Entropy vs. Gini: A Comparative Analysis for Decision Trees
Compare two popular impurity measures—Entropy and Gini Impurity—used in decision tree algorithms. Understand their differences, advantages, and when to use each in machine learning.
// import ‘katex/dist/katex.min.css’
Entropy vs. Gini: A Comparative Analysis for Decision Trees
1. Introduction
When constructing decision trees, selecting the right split at each node is crucial. Two popular criteria used to evaluate splits are Entropy and Gini Impurity. Both measures quantify the impurity of a dataset, but they differ in their mathematical formulation and computational complexity. This post explores these two metrics, compares their properties, and provides practical examples to help you decide which one to use.
2. What is Entropy?
Entropy originates from information theory and measures the amount of uncertainty or disorder in a dataset. In the context of decision trees, it quantifies the impurity of a node. The formula for entropy is:
Key Points:
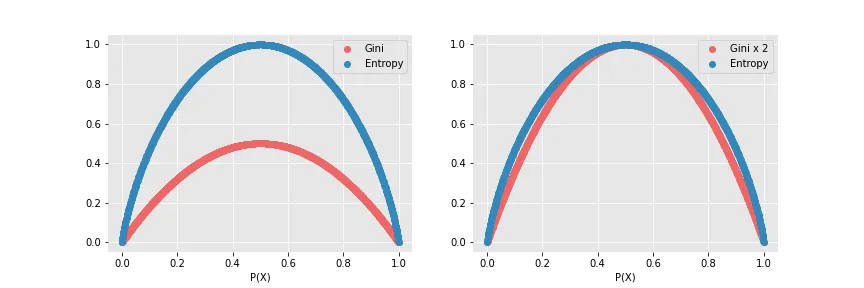
- Range: For binary classification, entropy ranges from 0 (pure) to 1 (maximum impurity).
- Interpretation: Higher entropy indicates more disorder (i.e., a mix of classes), while lower entropy suggests that one class dominates.
- Usage: Entropy is used in algorithms like ID3 and C4.5.
3. What is Gini Impurity?
Gini Impurity is another metric for assessing node purity. It measures the probability of misclassifying a randomly chosen element if it were labeled according to the distribution in the node. The formula for Gini Impurity is:
Key Points:
- Range: In binary classification, Gini impurity ranges from 0 (pure) to 0.5 (maximum impurity).
- Interpretation: A lower Gini value means a node is more pure.
- Usage: Gini is commonly used in CART (Classification and Regression Trees) due to its computational efficiency.
4. Comparing Entropy and Gini
| Aspect | Entropy | Gini Impurity |
|---|---|---|
| Formula | $-\sum p(x) \log_2 p(x)$ | $1 - \sum p(x)^2$ |
| Range (Binary) | 0 to 1 | 0 to 0.5 |
| Computation | Involves logarithms, slightly more complex | Simpler and computationally faster |
| Interpretability | Rooted in information theory | More intuitive for measuring misclassification probability |
| Usage in Trees | Used in ID3 and C4.5 algorithms | Used in CART algorithms |
Which One to Choose?
- Entropy is ideal when you want a measure based on information theory and are not constrained by computational resources.
- Gini Impurity is favored for its simplicity and speed, especially with large datasets, without a significant loss in performance.
5. Practical Example in Python
Below is a simple Python example demonstrating how to compute both Entropy and Gini Impurity for a given probability distribution.
5.1. Importing Libraries
import numpy as np5.2. Defining the Functions
def calculate_entropy(probabilities):
"""
Calculate the entropy of a probability distribution.
Parameters:
probabilities (list or np.array): Probabilities for each class.
Returns:
float: Entropy value.
"""
probabilities = np.array(probabilities)
# Filter out zero probabilities to avoid log2(0)
probabilities = probabilities[probabilities > 0]
return -np.sum(probabilities * np.log2(probabilities))
def calculate_gini(probabilities):
"""
Calculate the Gini Impurity of a probability distribution.
Parameters:
probabilities (list or np.array): Probabilities for each class.
Returns:
float: Gini Impurity value.
"""
probabilities = np.array(probabilities)
return 1 - np.sum(probabilities ** 2)5.3. Example Usage
# For a perfectly balanced binary classification:
prob_dist = [0.5, 0.5]
entropy_val = calculate_entropy(prob_dist)
gini_val = calculate_gini(prob_dist)
print("Entropy:", entropy_val) # Expected output: 1.0
print("Gini Impurity:", gini_val) # Expected output: 0.5
# For a skewed binary distribution:
prob_dist_skewed = [0.8, 0.2]
entropy_val_skewed = calculate_entropy(prob_dist_skewed)
gini_val_skewed = calculate_gini(prob_dist_skewed)
print("Entropy (skewed):", entropy_val_skewed)
print("Gini Impurity (skewed):", gini_val_skewed)6. Conclusion
Both Entropy and Gini Impurity are valuable metrics for evaluating splits in decision trees. While Entropy provides a theoretical foundation based on information theory, Gini Impurity offers a computationally simpler alternative. The choice between them often comes down to the specific requirements of your application and the trade-off between interpretability and computational efficiency.
Happy modeling!