Lasso vs Ridge Regression: A Comparative Guide

1. Introduction

Regularization techniques are essential for preventing overfitting in linear models. Two of the most popular methods are Lasso (L1 regularization) and Ridge (L2 regularization) regression. In this post, we compare these techniques, discuss their key differences, and provide a practical example using Python.

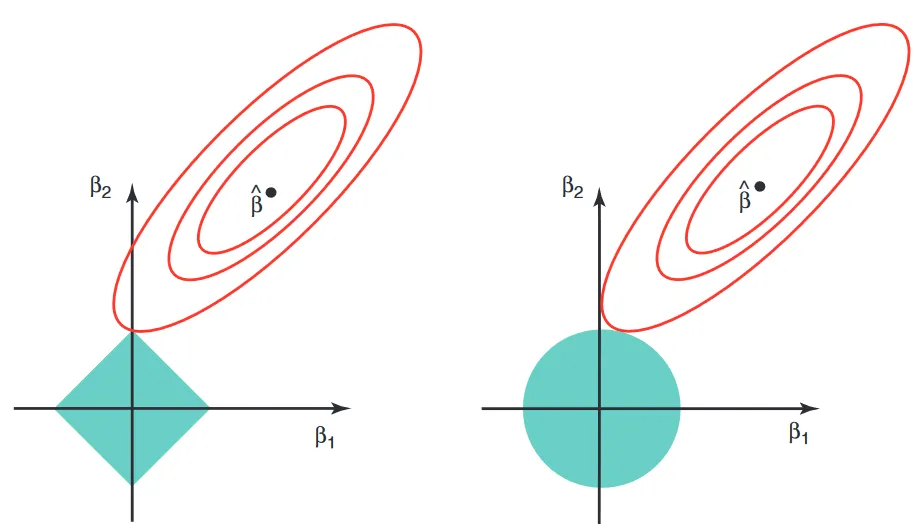
2. Understanding Lasso and Ridge Regression

Both Lasso and Ridge add a penalty term to the ordinary least squares loss function to constrain the model coefficients:

• Ridge Regression:
  Adds an L2 penalty proportional to the square of the magnitude of the coefficients. This approach shrinks the coefficients toward zero but rarely sets any of them exactly to zero.

• Lasso Regression:
  Adds an L1 penalty proportional to the absolute value of the coefficients. This penalty can force some coefficients to become exactly zero, effectively performing feature selection.

3. Key Differences

3.1. Feature Selection

• Lasso:
  Can reduce some coefficients to zero, making it useful for feature selection and creating simpler models.

• Ridge:
  Retains all features by shrinking their coefficients. It is more effective when most features contribute to the outcome.

3.2. Handling Multicollinearity

• Ridge:
  Particularly useful when dealing with multicollinearity as it distributes the penalty among correlated features.

• Lasso:
  May arbitrarily select one feature over another when features are highly correlated.

3.3. Model Complexity

• Lasso:
  Best suited for situations where you expect only a few features to be significant.

• Ridge:
  Works well when most or all features are believed to contribute to the prediction.

4. Implementing Lasso and Ridge in Python

Below is a practical example using the scikit-learn library with the diabetes dataset.

4.1. Importing Libraries

from sklearn.datasets import load_diabetes
from sklearn.linear_model import Lasso, Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as 

4.2. Loading and Splitting the Dataset

# Load the diabetes dataset
data = load_diabetes()
X, y = data.data, data.target

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

4.3. Training Lasso and Ridge Models

# Initialize models with a regularization parameter alpha
lasso = Lasso(alpha=0.1)
ridge = Ridge(alpha=1.0)

# Fit the models on the training data
lasso.fit(X_train, y_train)
ridge.fit(X_train, y_train)

4.4. Evaluating the Models

# Predict on the test set
lasso_pred = lasso.predict(X_test)
ridge_pred = ridge.predict(X_test)

# Calculate Mean Squared Error
lasso_mse = mean_squared_error(y_test, lasso_pred)
ridge_mse = mean_squared_error(y_test, ridge_pred)

print("Lasso MSE:", lasso_mse)
print("Ridge MSE:", ridge_mse)

4.5. Comparing Coefficients

print("Lasso coefficients:")
print(lasso.coef_)

print("Ridge coefficients:")
print(ridge.coef_)

Conclusion

Both Lasso and Ridge regression have unique strengths:

Use Lasso when you need feature selection or suspect that only a subset of features is important. Opt for Ridge when all features contribute to the outcome and you require a more stable solution in the presence of multicollinearity. Experiment with different values of the regularization parameter alpha to fine-tune your model. Happy modeling!